Ventilation Prediction for an Industrial Cement Raw Ball Mill by BNN—A “Conscious Lab” Approach
Download Article in PDF format
Rasoul Fatahi 1, Rasoul Khosravi 2, Hossein Siavoshi 3, Samaneh Yazdani 4, Esmaiel Hadavandi 5 and Saeed Chehreh Chelgani 6, *
- 1 School of Mining Engineering, College of Engineering, University of Tehran, Tehran 16846-13114, Iran; rasoul.fatahi95@gmail.com
- 2 Department of Mining, Faculty of Engineering, Lorestan University, Khorramabad 68151-44316, Iran; rlkhosravi@gmail.com
- 3 Department of Mining and Geological Engineering, University of Arizona, Tucson, AZ 85721, USA; hosseinsiavoshi@email.arizona.edu
- 4 Department of Electrical and Computer Engineering, North Tehran Branch, Islamic Azad University, Tehran 16511-53311, Iran; s_yazdani@iau-tnb.ac.ir
- 5 Department of Industrial Engineering, Birjand University of Technology, Birjand 97198-66981, Iran; es.hadavandi@gmail.com
- 6 Minerals and Metallurgical Engineering, Department of Civil, Environmental and Natural Resources Engineering, Luleå University of Technology, SE-971 87 Luleå, Sweden
- * Correspondence: saeed.chelgani@ltu.se
Abstract: In cement mills, ventilation is a critical key for maintaining temperature and material transportation. However, relationships between operational variables and ventilation factors for an industrial cement ball mill were not addressed until today. This investigation is going to fill this gap based on a newly developed concept named “conscious laboratory (CL)”. For constructing the CL, a boosted neural network (BNN), as a recently developed comprehensive artificial intelligence model, was applied through over 35 different variables, with more than 2000 records monitored for an industrial cement ball mill. BNN could assess multivariable nonlinear relationships among this vast dataset, and indicated mill outlet pressure and the ampere of the separator fan had the highest rank for the ventilation prediction. BNN could accurately model ventilation factors based on the operational variables with a root mean square error (RMSE) of 0.6. BNN showed a lower error than other traditional machine learning models (RMSE: random forest 0.71, support vector regression: 0.76). Since improving the milling efficiency has an essential role in machine development and energy utilization, these results can open a new window to the optimal designing of comminution units for the material technologies.
Keywords: cement; ball mill; conscious laboratory; random forest; support vector regression.
[1] . Introduction
In the cement industry, grinding is one of the most consuming energy stages in the production units. Around 65% of the total used electrical energy in a cement plant has to be utilized to grind raw materials, coal, and clinker [1,2]. Through the process, many variables can affect the efficiency and productivity of this dry grinding procedure, such as the operating conditions of the separators, airflow through the mill, the aperture size of the mill partitions, feed rate, the hardness of the feed material, and ball sizes in the mill compartments. Understanding the relationships between these variables from the grinding units can play an essential role in efficiently operating cement production lines [3–5].
One of the most critical variables in the cement ball mills is ventilation. A mixture of hot and recycled air would deliver and dry the powder in a cement ball mill as a pulverizing system. Thus, ventilation in this system can have a significant effect on the production process. Extensive ventilation can substantially increase the coarse powder, while in the small ventilation, the delivered powder decreases (as a result, the output decreases). Only proper ventilation ensures the max output with qualified powder, and reduces loss [6–8]. The multiphase character of flow made the ventilation controlling an essential factor (where recirculation gases, pulverized coal, sand, and other materials are included) [6–9]. In detail, there are many parameters in a cement ball mill that may influence the ventilation. The ball mill load, the outlet temperature, the hot air pressure, the recycle air pressure, the negative inlet pressure, the different inlet-outlet pressure, and the outlet pressure of the fine and coarse separators are just some of those influential variables [6–10]. However, few studies have explored the possible relationships between operating variables and ventilation for an industrial ball mill in a cement plant [11,12].
For assessing complex relationships among a wide range of variables monitored from the industrial plants, constructing advanced artificial intelligence (AI) models based on the existing data could be a key to better measure the importance of variables. The development of such reliable models as a new concept recently has been called “consciouslaboratory (CL)”. Generating a CL by using a robust AI model can reduce cost, save time, improve the controlling system, and remove scale-up challenges [13,14]. However, few investigations have used AI models in the cement industry to explore correlations among operational variables [15,16], and absolutely no study has considered a CL for analyzing the effect of various operating variables on mill ventilation. This study will introduce a CL developed by Boosted Neural Network (BNN) as a recently construct AI model to fill the gap. For the first time, this work addresses the importance and effectiveness of all monitored variables on the mill ventilation, based on the actual monitored data from line one of the Ilam cement plant (Ilam, Iran) by a BNN model. The BNN prediction results were compared to two other traditional advanced AI models (random forest and support vector regression) for accuracy assessment purposes.
- Materials and Methods
2.1. Database
To investigate relationships between various measured variables and ventilation rate, the data were collected from one of the Raw Material ball mill circuits (line 1) of the Ilam cement plant (Figure 1). This plant has 2 lines for cement production (5300 t/d). The ball mill has one component, 5.20 m diameter, and 11.20 m length with 240 t/h capacity (made by PSP Company from Prˇerov, Czechia). The mill’s rotation speeds are mainly constant (14 rpm), and there is approximately a fixed one-year period of changing liners. Various parameters are monitored in this unit (Table 1). Variables were hourly monitored and were taken into account (when the circuit was stable and balanced). In general, over 2000 records were used for the modeling. Regularly measuring pressure before and after the mill fan (PBMF and PAMF, respectively) can be considered as ventilation factors in a mill.
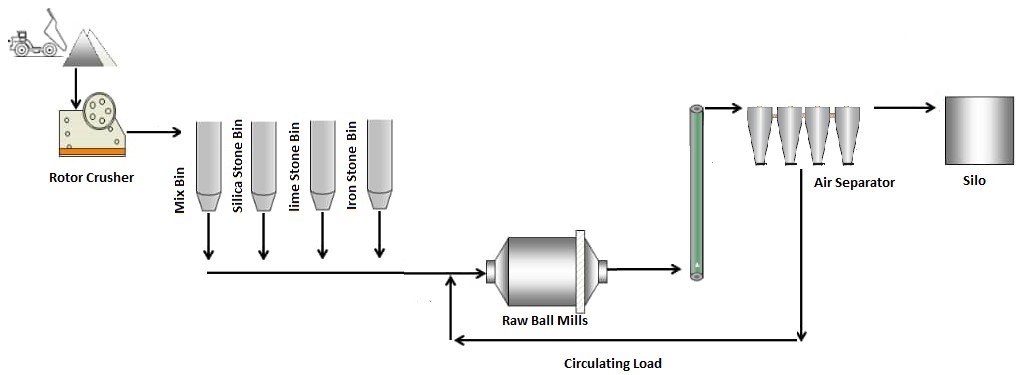
Figure 1. Schematic of ball mill circuit in the Ilam cement plant.
Table 1. Descriptive statistics of monitored variables in the plant.
| Variables | Minimum | Maximum | Mean | Std. Deviation |
| Temperature of exhaust electro filter ◦C | 50 | 260 | 119.90 | 12.85 |
| HVP (1) (KV) | 7 | 596 | 62.90 | 129.80 |
| HVP (2) (KV) | 31 | 74 | 67.00 | 3.60 |
| Electro filter duct pressure (mbar) | 1 | 41 | 14.33 | 1.99 |
| Inlet electro filter temperature ◦C | 44 | 173 | 106.14 | 7.55 |
| Electro filter damper fan (%) | 15 | 100 | 98.93 | 7.49 |
| Electro filter fan (A) | 22 | 89 | 38.75 | 3.47 |
| Mill fan duct temperature ◦C | 2 | 115 | 79.39 | 7.50 |
| After mill fan pressure (mbar) | 4 | 18 | 7.52 | 1.32 |
| Before mill fan (mbar) | 39 | 64 | 53.88 | 2.30 |
| Mill fan motor (A) | 6 | 84 | 62.33 | 2.48 |
| Mill fan damper (%) | 80 | 100 | 99.90 | 1.25 |
| Hot air damper (%) | 46 | 100 | 57.30 | 11.82 |
| Separator rotor (rpm) | 17 | 50 | 22.64 | 3.92 |
| After separator fan pressure (mbar) | 0 | 109 | 2.28 | 2.52 |
| Total feed (ton) | 18 | 230 | 191.01 | 17.67 |
| Mix bin feeders (ton) | 18 | 220 | 180.1 | 18.95 |
| Damper of separator fan (%) | 35 | 95 | 51.75 | 6.79 |
| Before mill fan pressure (mbar) | 9 | 73 | 14.17 | 2.48 |
| Separator outlet temperature ◦C | 43 | 112 | 73.63 | 7.79 |
| Separator fan (A) | 26 | 180 | 29.94 | 3.45 |
| Separator motor (A) | 12 | 1173 | 119.56 | 23.49 |
| Airlift blower2 (A) | 15 | 264 | 170.84 | 12.05 |
| Airlift blower1 (A) | 17 | 198 | 172.76 | 11.18 |
| Buck elevator motor2 (A) | 40 | 87 | 54.54 | 3.15 |
| Buck elevator motor1 (A) | 42 | 72 | 53.88 | 4.00 |
| Main motor2 (A) | 23 | 841 | 241.36 | 20.50 |
| Main motor1 (A) | 205 | 2369 | 241.39 | 47.23 |
| Mill outlet pressure (mbar) | 24 | 369 | 35.63 | 7.85 |
| Mill inlet pressure (mbar) | 2 | 14 | 9.59 | 0.96 |
| Main gearbox2 temperature ◦C | 12 | 60 | 35.79 | 6.63 |
| Main gearbox1 temperature ◦C | 14 | 56 | 40.90 | 5.97 |
| Outlet bearing temperature ◦C | 30 | 64 | 51.37 | 5.52 |
| Inlet bearing temperature ◦C | 28 | 59 | 44.80 | 4.85 |
| Mill outlet temperature ◦C | 41 | 124 | 80.29 | 7.30 |
| Mill inlet temperature ◦C | 69 | 498 | 281.90 | 22.48 |
| Circulating load (ton) | 4 | 468 | 143.03 | 64.47 |
2.2. AI Models
2.2.1. Boosted Neural Network
As a powerful artificial intelligence (AI) model, Boosted Neural Network (BNN) was constructed using neural network experts and ensemble algorithm. BNN promotes the probability of sampling data for training experts in predictive functions. It improves the verification of balance through the training dataset by conducting a wide distribution of inputs and decreasing prediction errors by considering previous experts’ prediction information [17–20]. It can linearly and nonlinearly examine relationships among a dataset by assessing multivariable sensitivity analyses (MSA), evaluate the sensivity of output to the given inputs, indicate magnitudes, and rank variables based on their importance [20]. In this work, the BNN’s marginal model (MM) was used for the MSA assessments. In the BNN-MM, inputs are ordered based on the size of their overall total effect importance indices [21]. BNN can reduce the objective function (Equation (1)) for the traning step [22], as follows:
Et WTt Wt (1)
where N is the number of samples in the training dataset, y is the target value, yˆ is the predicted value by t-th, experts, and α is the parameter, which is between 0 and 1. Wt is the weight vector of t-th neural network expert in the BNN.
2.2.2. Random Forest
As a tree-based statistical model, random forest (RF) was constructed and developed by Breiman et al. (1993) [23]. A powerful AI machine learning (ML) model can provide low-bias and low-variation outcomes, with highly accurate predictions [24–27]. In this system, an estimated value generates according to the average of overall trees through the bagging system; different bootstrap data L(θ) with size n would be selected from the training set (L) with size N. Each tree “TL(θ)” would be related to the random vector θ, which is given for the bagged samples from the main training set L. The final predictor “f” is the average over the forest (with y’η the estimated response for sample xη where K is the size of the ensemble) [28–30], as follows:
y f X (2)
2.2.3. Support Vector Regression
Support vector regression (SVR) has been developed based on the structural risk minimization (SRM) principle from statistical learning theory. Regarding the SRM principle, SVR can reduce the risk of overfitting in prediction and generate a compressive model by taking the information of all outputs for the prediction [31–33]. SVR can transfer a complex nonlinear regression problem to a linear regression problem in a high dimensional variable space. In other words, a linear function f (SVR function) can be used to formulate the nonlinear relationship between Xi and Yi, as follows:
f(x) = wϕ(x)+ b (3)
where f(x) shows the predicted value, and the two parameters w ∈ <nh and b ∈ < must be adjusted. For SRM, empirical risk Equation (4) can be considered where ε (ε-insensitive) is a precision parameter representing the radius of the tube located around the regression function [33,34].
| minRe(w, ξ ∗, ξ) = |w|2 + C ∑(ξ ∗ +ξ)
2 i=1 With the following constraints: |
(4) |
1 n
1, 2, 3, . . . n
(5)
−yi + wϕ(xi)+ b ≤ ε+ξi i = 1, 2, 3, . . . n
n
ξi ≥ 0 i = 1, 2, 3, . . . n
- Results and Discussion
3.1. Variable Importance Measurement
For the variable importance measurement, BNN-MM considers the mean response of the target for each predictor record. The mean is taken over all inputs for the calculation of the importance indices. BNN-MM assessments among monitored variables in the plant indicated that the mill outlet pressure had the highest effectiveness (rank) on the PBMF prediction. There was a positive correlation between these two factors (Figure 2). For the PAMF prediction, the ampere of the separator fan had the highest rank, and by increasing its ampere, the pressure after the mill fan was decreased (a negative relationship) (Figure 2). These relationships could be because fan capacity can limit the separator fan capacity, and pulling more air can increase the separator capacity when the mill separator was not running at its maximum speed [35]. Zachariades (2015) indicated that the differential pressure in the mill is proportional to the primary air fan, which was produced the differential pressure [36].
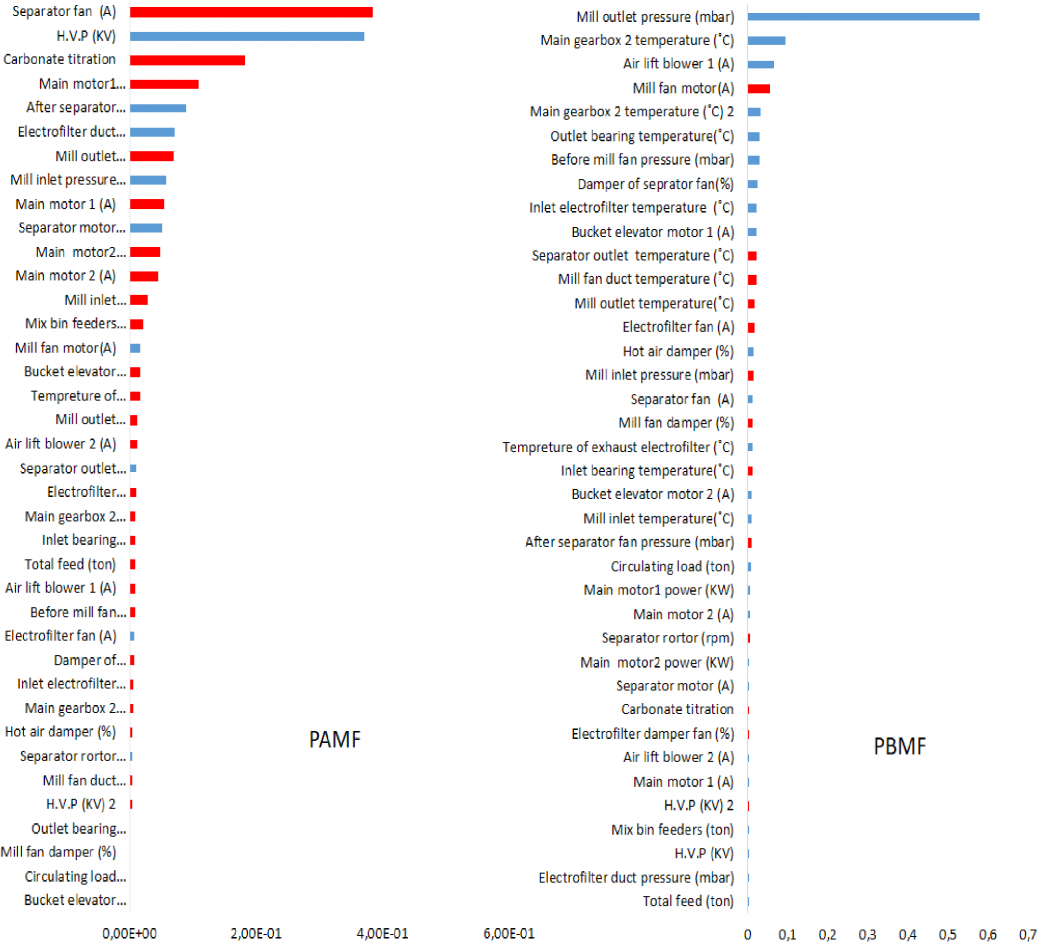
Figure 2. Variable importance measurement for ranking variables. Pearson correlation: Positive (blue), negative (red).
3.2. Prediction
The samples of records (1870) were randomly applied for the training stage from the database, and the rest of the records (198) were used for the testing step. For constructing the most accurate predictive BNN model, a trial and error practice was considered to obtain the number of experts. The robust BNN model was generated by the five neural network experts. The developed BNN model expert was a one-layer perceptron neural network with four hidden neurons and a ‘tanh’ activation function. The back-propagation learning algorithm was applied for the training of the experts. The BNN outcomes (Table 2) showed that the developed CL by BNN could comprehensively predict both PAMF and PBMF based on the plant’s monitored parameters. For evaluation purposes, precisely the same databases that were used for constructing the CL-BNN were applied for the development of RF and SVR modeling as typical ML methods. The results (Figure 3) demonstrated that BNN could provide higher accuracy for the PAMF and PBMF prediction than these traditional ML methods. These outcomes highlighted the potential of CL for controlling, sustaining, and estimating other essential variables within cement plants.
Table 2. Statistical indexes for the outcomes of the training step from different models.
| PAMF | PBMF | |||
| Model | MAE | RMSE | MAE | RMSE |
| BNN | 0.43 | 0.60 | 0.77 | 1.06 |
| SVR | 0.45 | 0.76 | 0.98 | 1.46 |
| RF | 0.48 | 0.71 | 0.91 | 1.31 |
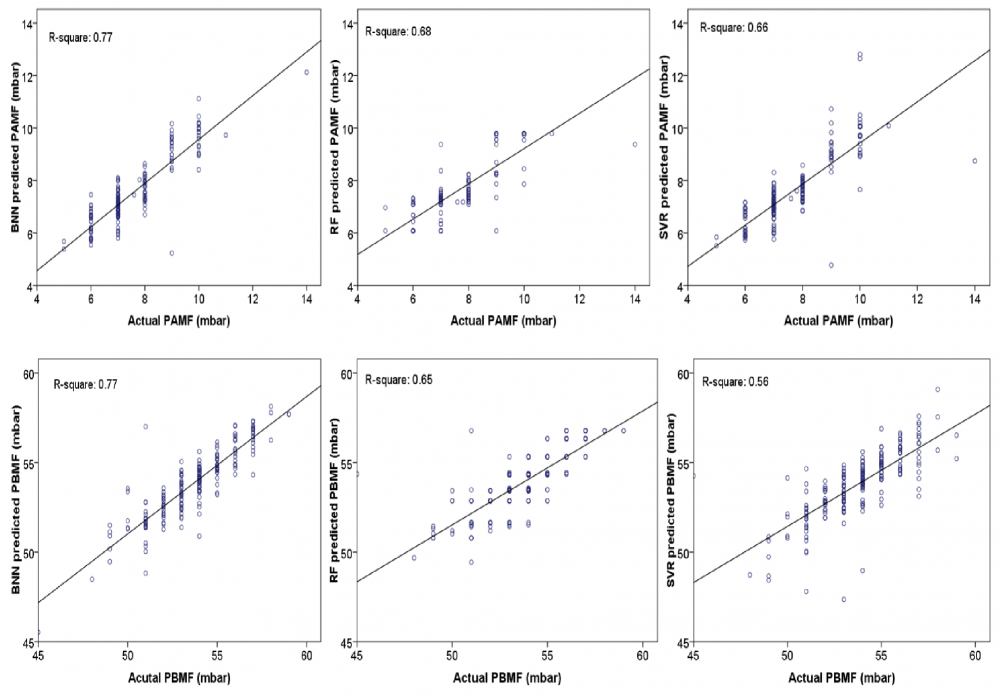
Figure 3. Coefficient of determination (R-square) for the different model outcomes in the testing stage.
-
Conclusions
As a virtual laboratory, the development of a conscious-laboratory can be an essential step for maintaining and controlling an industrial plant. For the first time, this study explored the relationships between operational variables and ventilation factors for an industrial cement ball mill, and developed a conscious lab by BNN as a newly generated AI model. Variable importance assessments indicated that the mill outlet pressure and the separator fan’s ampere had the highest importance for predicting ventilation factors. Assessing relationship magnitudes showed that operating variables might have reverse effects on ventilation parameters; however, the mill outlet’s pressure positively correlates with the ventilation factors. In a dry grinding system, the BNN results showed that ventilation, as an efficient factor, could be accurately predicted through a conscious lab procedure. BNN could accurately predict the measuring pressure before and after the mill fan, with R2 = 0.77. A comparison between BNN outcomes and random forest/support vector regression, R2 < 0.70, approved this newly developed model’s accuracy. These considerable outcomes indeed stressed the possibility of automatic maintenance through cement plants’ operation, where the conscious lab principle showed its reliability for the monitored data assessments.
Author Contributions: Conceptualization, S.C.C. and R.F.; methodology, S.C.C. and R.F.; software, S.Y. and E.H.; validation, S.C.C., R.F. and E.H.; formal analysis, S.C.C.; investigation, R.K. and H.S.; resources, R.K. and H.S.; data curation, R.K. and H.S.; writing—original draft preparation, S.C.C.;
writing—review and editing, S.C.C. and R.F.; visualization, S.Y. and E.H.; supervision, S.C.C.; project administration, R.F. All authors have read and agreed to the published version of the manuscript.
Funding: This research received no external funding.
Institutional Review Board Statement: Not applicable.
Informed Consent Statement: Not applicable.
Data Availability Statement: Data available on request due to restrictions e.g., privacy or ethical.
Acknowledgments: The first author’s appreciation goes to Ilam cement plant management for providing access to production line one circuit the plant.
Conflicts of Interest: The authors declare no conflict of interest.
References
- Jankovic, A.; Valery, W.; Davis, E. Cement grinding optimisation. Eng. 2004, 17, 1075–1081. [CrossRef]
- Oss, H.G.; Padovani, A.C. Cement Manufacture and the Environment Part II: Environmental Challenges and Opportunities. Ind. Ecol. 2003, 7, 93–126. [CrossRef]
- Lynch, A.J.; Bush, P. Mineral Crushing and Grinding Circuits: Their Simulation, Optimisation, Design and Control; Elsevier: Amsterdam, The Netherlands, 1977.
- Ghalandari, V.; Iranmanesh, A. Energy and exergy analyses for a cement ball mill of a new generation cement plant and optimizing grinding process: A case study. Powder Technol. 2020, 31, 1796–1810. [CrossRef]
- Ghalandari, V.; Esmaeilpour, M.; Payvar, N.; Reza, M.T. A case study on energy and exergy analyses for an industrial-scale vertical roller mill assisted grinding in cement plant. Powder Technol. 2021, 32, 480–491. [CrossRef]
- Perkovic´, B.; Mazurkijevicˇ, A.; Tarasek, V.; Stevic´, L. TTP Kostolac unit 2 refurbishment and improvement aiming to obtained designed production. Termotehnika 2004, 30, 57–81.
- Kozic, M.; Ristic, S.; Puharic, M.; Katavic, B. Numerical simulation of multiphase flow in ventilation mill and channel with louvers and centrifugal separator. Sci. 2011, 15, 677–689. [CrossRef]
- Gulicˇ, M. Calculation of Fan Mill, Beograd. 1982.
- Yuan, Y.; Zhang, Y.; Cao, H.; Si, G.; Zhang, S.; Xie, Q. Nonlinear prediction model for ventilation of ball mill pulverizing system. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, Chian, 27–29 July 2016; pp. 2025–2028. [CrossRef] Özer, C.; Ergün, S.; Benzer, A. Modeling of the classification behavior of the diaphragms used in multi-chamber cement mills. Int.
- Miner. Process. 2006, 80, 58–70. [CrossRef]
- Altun, O.; Benzer, H.; Dundar, H.; Aydogan, N.A. Comparison of open and closed circuit HPGR application on dry grinding circuit performance. Eng. 2011, 24, 267–275. [CrossRef]
- Stanišic´, D.; Jorgovanovic´, N.; Popov, N.; Congradac, V. Soft sensor for real-time cement fineness estimation.ˇ ISA Trans. 2015, 55, 250–259. [CrossRef]
- Tohry, A.; Yazdani, S.; Hadavandi, E.; Mahmudzadeh, E.; Chelgani, S.C. Advanced modeling of HPGR power consumption based on operational parameters by BNN: A “Conscious-Lab” development. Powder Technol. 2021, 381, 280–284. [CrossRef]
- Alidokht, M.; Yazdani, S.; Hadavandi, E.; Chelgani, S.C. Modeling metallurgical responses of coal Tri-Flo separators by a novel BNN: A “Conscious-Lab” development. J. Coal Sci. Technol. 2021, 1–11. [CrossRef]
- Ozdemir, A.C.; Dag, A.; Ibrikci, T. A Comparative Assessment on Cement Raw Material Quarry Quality Distribution via 3-D Identification. Min. Sci. 2018, 54, 609–616. [CrossRef]
- Seraj, M.; Shooredeli, M.A. Data-driven predictor and soft-sensor models of a cement grate cooler based on neural network and effective dynamics. Conf. Electr. Eng. 2017, 2017, 726–731. [CrossRef]
- Hadavandi, E.; Shahrabi, J.; Hayashi, Y. SPMoE: A novel subspace-projected mixture of experts model for multi-target regression problems. Soft Comput. 2015, 20, 2047–2065. [CrossRef]
- Hadavandi, E.; Shahrabi, J.; Shamshirband, S. A novel Boosted-neural network ensemble for modeling multi-target regression problems. Appl. Artif. Intell. 2015, 45, 204–219. [CrossRef]
- Golzadeh, M.; Hadavandi, E.; Chelgani, S.C. A new Ensemble based multi-agent system for prediction problems: Case study of modeling coal free swelling index. Soft Comput. J. 2018, 64, 109–125. [CrossRef]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression; Sage Publications: Thousand Oaks, CA, USA, 2018.
- Carver, R. Practical Data Analysis with JMP; SAS Institute: Cary, NC, USA, 2019.
- Chelgani, S.C.; Hadavandi, E.; Hower, J.C. Estimation of heavy and light rare earth elements of coal by intelligent methods. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 43, 70–79. [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall/CRC: London, UK, 1984.
- Matin, S.; Hower, J.C.; Farahzadi, L.; Chelgani, S.C. Explaining relationships among various coal analyses with coal grindability index by Random Forest. J. Miner. Process. 2016, 155, 140–146. [CrossRef]
- Chelgani, S.C.; Matin, S.; Makaremi, S. Modeling of free swelling index based on variable importance measurements of parent coal properties by random forest method. J. Int. Meas. Confed. 2016, 94, 416–422. [CrossRef]
- Shahbazi, B.; Chelgani, S.C.; Matin, S. Prediction of froth flotation responses based on various conditioning parameters by Random Forest method. Colloids Surfaces A Physicochem. Eng. Asp. 2017, 529, 936–941. [CrossRef]
- Nazari, S.; Chelgani, S.C.; Shafaei, S.; Shahbazi, B.; Matin, S.; Gharabaghi, M. Flotation of coarse particles by hydrodynamic cavitation generated in the presence of conventional reagents. Purif. Technol. 2019, 220, 61–68. [CrossRef]
- Chelgani, S.C.; Matin, S.S. Study the relationship between coal properties with Gieseler plasticity parameters by random forest. J. Oil Gas Coal Technol. 2018, 17, 113–127. [CrossRef]
- Tohry, A.; Chelgani, S.C.; Matin, S.; Noormohammadi, M. Power-draw prediction by random forest based on operating parameters for an industrial ball mill. Powder Technol. 2020, 31, 967–972. [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Neural Inf. Process. Syst. 1996, 9, 155–161.
- Chelgani, S.C.; Shahbazi, B.; Hadavandi, E. Support vector regression modeling of coal flotation based on variable importance measurements by mutual information method. J. Int. Meas. Confed. 2018, 114, 102–108. [CrossRef]
- Hadavandi, E.; Hower, J.C.; Chelgani, S.C. Modeling of gross calorific value based on coal properties by support vector regression method. Earth Syst. Environ. 2017, 3, 37. [CrossRef]
- Hadavandi, E.; Chelgani, S.C. Estimation of coking indexes based on parental coal properties by variable importance measurement and boosted-support vector regression method. J. Int. Meas. Confed. 2019, 135, 306–311. [CrossRef]
- Chelgani, S.C.; Hadavandi, E.; Hower, J.C. Study Relationship Between the Coal Thermoplastic Factor With Its Organic and Inorganic Properties by the Support Vector Regression Method. J. Coal Prep. Util. 2020, 40, 743–754. [CrossRef]
- McKervey, G.; Perry, B. Fan applications in cement industry. IEEE Cem. Ind. Tech. Conf. 1993, 467–476.
Zachariades, P. Development of a Tube-Ball Mill Mathematical Model for Mill Condi-tion and Safety Monitoring. Ph. D. Thesis, University of Birmingham, Birmingham, UK, 2015.
